ნიკოლოზ ჩხაიძე
შეფასებისა და გამოცდების ეროვნული ცენტრის ფიზიკის ჯგუფის წარმომადგენელი
დღეს გესაუბრებით ფიზიკის საგამოცდო ტესტის შესახებ. შეიცვალა ტესტის ფორმატი, ადრე 75-ქულიანი იყო, წელს 63-ქულიანია, შესაბამისად, დროც შემცირდა, სამსაათ-ნახევრის ნაცვლად, 3 საათი ეთმობა.
შეფასებისა და გამოცდების ეროვნული ცენტრის ვებგვერდზე დევს წელს გამოცემული კრებული აბიტურიენტებისთვის, სადაც თქვენ შეგიძლიათ ნახოთ როგორც საგამოცდო პროგრამა (რა საკითხების ცოდნა მოგეთხოვებათ გამოცდაზე), ასევე ის უნარ-ჩვევები, რომლებიც მოწმდება გამოცდაზე, აგრეთვე გასული წლის ტესტი (სწორი პასუხები, შეფასების სქემები) და 63-ქულიანი, ახალი ფორმატის ტესტი, ასევე, სწორი პასუხებითა და შეფასების სქემებით.
უნდა აღინიშნოს, რომ 63-ქულიან ტესტში რაც გვიდევს, ეს ძველი, სხვადასხვა წელს გამოცდაზე გასული ამოცანებიდან არის აღებული, უბრალოდ ფორმატს მოვარგეთ, დაახლოებით, როგორი იქნება 63-ქულიანი ტესტი. ამოცანები, დონით, ზოგი უფრო მარტივია, ზოგი — უფრო რთული. ვიმეორებ, ეს არ გახლავთ სპეციალურად ახალი გამოცდისთვის მომზადებული ტესტი. ამ ტესტის ზოგიერთი ამოცანის მაგალითზე, გავამახვილებ თქვენს ყურადღებას მნიშვნელოვან მომენტებზე.
ტესტში ამოცანების სახეები ისეთივეა, როგორიც აქამდე იყო. როგორც გახსოვთ, დავალებები სამი ტიპის იყო: დავალებები, რომლებშიც არის 5 არჩევითი პასუხი და იქიდან ერთადერთია მხოლოდ სწორი; იყო ე.წ. შესაბამისობის ტიპის დავალებები, სადაც ობიექტების ერთ ჯგუფს უნდა შეუსაბამოთ რაღაც ობიექტი სხვა ჩამონათვალიდან, ანუ ერთი ჩამონათვალის ობიექტს უნდა შევუსაბამოთ სხვა ჩამონათვალის რომელიმე ობიექტი. არის შემთხვევები, როდესაც შეიძლება შესაბამისი ობიექტი არ მოიძებნოს, ამ შემთხვევაში, უჯრას დატოვებთ ცარიელს, შეუვსებელს. თუ მოხდა ისე, რომ ერთ ობიექტს შეესაბამება რამდენიმე ობიექტი (ეს ჯერ არ მომხდარა), მაშინ ყველა ის ობიექტი უნდა იპოვოთ, მაგალითად, წერია — ენერგიას შეუსაბამეთ რაღაც ერთეულები და ერთეულებში არის ჯოულიც და ნიუტონ-მეტრიც, ერთიც შეესაბამება ენერგიას და მეორეც, მაგრამ, ვიმეორებ, ასეთი რამ იშვიათად ყოფილა, სამაგიეროდ ბევრი ყოფილა ისეთი, როდესაც რომელიღაც ობიექტს არ მოეძებნოს შესაბამისი ერთეული, მაგალითად, ხახუნის კოეფიციენტი. როგორც იცით, ხახუნის კოეფიციენტი უერთეულო სიდიდეა და როცა ვამბობთ, ხახუნის კოეფიციენტს შეუსაბამეთ რომელიღაც ერთეული ჩამონათვალიდან, ცხადია, იქ არ მოიძებნება არც ერთი ერთეული, რომელიც ხახუნის კოეფიციენტს შეესაბამება და შესაბამისი უჯრაც შეუვსებელი დარჩება.
ახლა ერთ ღია ამოცანაზე ვისაუბროთ და იმ შეცდომებზე, რასაც აქ უშვებენ აბიტურიენტები. აი, გვაქვს ასეთი ამოცანა:
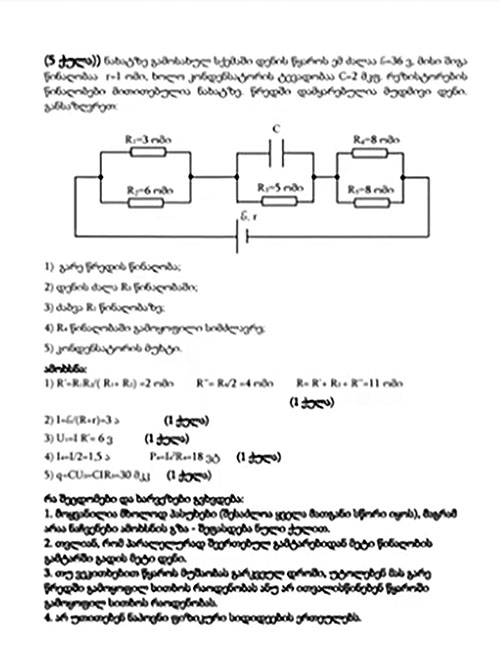 ხედავთ სქემას, რომელზეც გამოსახულია გარკვეული რეზისტორები, ერთ-ერთთან, პარალელურად, შეერთებულია კონდენსატორი და დენის წყარო. მოცემულია დენის წყაროს ელექტრომამოძრავებელი ძალა, მისი შიგა წინაღობა, კონდენსატორის ელექტროტევადობა, ყველა რეზისტორს აწერია თავისი წინაღობა და დავალება გვეუბნება: 1. იპოვეთ გარე წრედის წინაღობა, 2. დენის ძალა კონკრეტულად ერთ-ერთ წინაღობაში, 3. ძაბვა რომელიღაც სხვა წინაღობაზე, 4. ერთ-ერთ წინაღობაში გამოყოფილი სიმძლავრე და 5. კონდენსატორის მუხტი. პირობაში წერია — მას შემდეგ, რაც დენი დამყარდება. ასეთი ამოცანა იშვიათია აბიტურიენტებისთვის, მაგრამ ამ ამოცანის ამოხსნა თქვენს ძალებს სავსებით შეესაბამება.
ხედავთ სქემას, რომელზეც გამოსახულია გარკვეული რეზისტორები, ერთ-ერთთან, პარალელურად, შეერთებულია კონდენსატორი და დენის წყარო. მოცემულია დენის წყაროს ელექტრომამოძრავებელი ძალა, მისი შიგა წინაღობა, კონდენსატორის ელექტროტევადობა, ყველა რეზისტორს აწერია თავისი წინაღობა და დავალება გვეუბნება: 1. იპოვეთ გარე წრედის წინაღობა, 2. დენის ძალა კონკრეტულად ერთ-ერთ წინაღობაში, 3. ძაბვა რომელიღაც სხვა წინაღობაზე, 4. ერთ-ერთ წინაღობაში გამოყოფილი სიმძლავრე და 5. კონდენსატორის მუხტი. პირობაში წერია — მას შემდეგ, რაც დენი დამყარდება. ასეთი ამოცანა იშვიათია აბიტურიენტებისთვის, მაგრამ ამ ამოცანის ამოხსნა თქვენს ძალებს სავსებით შეესაბამება.
კონდენსატორში მუდმივი დენი, როგორც იცით, არ გადის, ვინაიდან ის არაგამტარია. უნდა მიხვდეთ, რომ მუდმივი დენის შემთხვევაში, დენი გადის მხოლოდ გამტარებით შედგენილ წრედში. ამიტომ, ცოტა ხნით, დაივიწყეთ კონდენსატორი, დაიწყეთ ამოხსნა. ახლა გიჩვენებთ, როგორ მიდის ამოხსნის თანმიმდევრობა: პოულობთ სრულ წინაღობას, იქ ორი ფარულად შეერთებული გამტარია, წერთ ფარული შეერთების ფორმულას, წერთ შედეგს. არავინ არ გთხოვთ, რომ მოიყვანოთ გამოთვლები ან ზუსტი ჩასმები გააკეთოთ (ეს შეიძლება შავ ფურცელზე გააკეთოთ). მთავარია, გზა იყოს სწორად მითითებული. ჩვენი მოთხოვნაა, ღია ამოცანებში, აუცილებლად, პასუხებთან ერთად, იყოს მოკლედ, მაგრამ ნათლად გადმოცემული პასუხის მიღების გზა, ანუ რა ფორმულა გამოიყენეთ ამ შედეგის მისაღებად, თვითონ გათვლა შეგიძლიათ შავ ფურცელზე გააკეთოთ, ოღონდ შედეგი უნდა შეიტანოთ და არ დაივიწყოთ ერთეულის მითითება. ფიზიკაში, მოგეხსენებათ, სიდიდეებს აქვთ ერთეულები. ერთ-ერთი შეცდომა არის ეს — ბევრს ერთეულების მითითება ავიწყდება.
აქ ამოხსნის გზა ასეთია: ნაპოვნია მეორე წინაღობა, მერე — მთელი წრედის წინაღობა, მერე გამოყენებულია ომის კანონი მთელი წრედისათვის და ნაპოვნია დენის ძალა, შემდეგ ნაპოვნია ერთ-ერთ უბანზე ძაბვა, რომელსაც კითხულობდნენ და ა.შ. თუ თქვენ ეს ფორმულები არ გიწერიათ და მხოლოდ სწორი პასუხები წერია, რა თქმა უნდა, ეს ნაწერი არ შეფასდება. ძალიან სამწუხარო იქნება, მაგრამ ეს ნამუშევარი არ შეფასდება იმიტომ, რომ მოთხოვნაა, ამოხსნის გზა ნათლად იყოს ნაჩვენები, ოღონდ მოკლედ.
რაც შეეხება კონდენსატორის ელექტროტევადობას, თქვენც მიხვდებით, რომ ნახაზზე, რომელიც თქვენ ცოტა ხნის წინ გიჩვენეთ, კონდენსატორი ფარულად არის შეერთებული R მესამე წინაღობის რეზისტორთან და ამიტომ მასზე ძაბვა იქნება იგივე, რაც რეზისტორზეა. ეს ძაბვა როდის წარმოიქმნა? ცხადია, მანამ, სანამ მუდმივი დენი დამყარდებოდა.
კიდევ ერთი შეცდომა — როცა ძაბვას ვეძებდით, მთელი ამ უბნისთვის გამოვიყენეთ ომის კანონი იმიტომ, რომ ნაპოვნი გვქონდა ფარული შეერთების წინაღობა, ნაპოვნი გვქონდა, ასევე, სრული დენი და ერთბაშად, ერთი ფორმულით ვიპოვეთ ძაბვა. ბევრი აკეთებს სხვა გზით, რომელიც აგრეთვე მისაღებია, მაგრამ რთულია — შემოყავთ დენის ძალები ამ გამტარებში და დენის ძალების ჯამი არის სრული დენი, ხოლო მათი შეფარდება, როგორც ვიცით, უნდა იყოს წინაღობების შებრუნებული შეფარდების ტოლი. თუ აბიტურიენტი ამ ორ განტოლებას დაწერს, აქედან მიიღებს დენის ძალებს და შემდეგ ძაბვას იანგარიშებს, რა თქმა უნდა, სრულად ჩაეთვლება, ოღონდ ეს უფრო გრძელი გზაა. ეცადეთ, მოკლე გზით ამოხსნათ ამოცანები. და კიდევ ერთი დამახასიათებელი შეცდომა, რომელიც აქ მოსდით (ალბათ უყურადღებობის ბრალია, ძალიან მნიშვნელოვანია გამოცდაზე ყურადღების მობილიზება) — ბევრი წერს, რომ დენის ძალების შეფარდება წინაღობების შეფარდების ტოლია, ანუ მიაჩნიათ, რომ 6-ომიანში მეტი დენის ძალა გადის, ვიდრე 3-ომიანში, რაც მცდარია.
ახლა შესაბამისობის ტიპის დავალებებზე გავამახვილებ თქვენს ყურადღებას. მაგალითად, გვაქვს ასეთი შესაბამისობის ტიპის დავალება:
 აქ აღწერილია ასეთი პროცესი — m მასის ბურთულა ბრუნავს უძრავი ღერძის გარშემო, R რადიუსიან წრეწირზე მუდმივი v სიჩქარით. იმპულსის მოდული აღნიშნულია P-თი, კინეტიკური ენერგია — E-თი, ძალების ტოლქმედი — F-ით. დაადგინეთ შესაბამისობა ციფრებით დანომრილ გამოსახულებებსა და ასოებით დანომრილ ფიზიკურ სიდიდეებს შორის. აბიტურიენტმა პასუხების ფურცელზე, სათანადო უჯრაში, უნდა შეიტანოს სათანადო სიმბოლო — X (ჯვარი).
აქ აღწერილია ასეთი პროცესი — m მასის ბურთულა ბრუნავს უძრავი ღერძის გარშემო, R რადიუსიან წრეწირზე მუდმივი v სიჩქარით. იმპულსის მოდული აღნიშნულია P-თი, კინეტიკური ენერგია — E-თი, ძალების ტოლქმედი — F-ით. დაადგინეთ შესაბამისობა ციფრებით დანომრილ გამოსახულებებსა და ასოებით დანომრილ ფიზიკურ სიდიდეებს შორის. აბიტურიენტმა პასუხების ფურცელზე, სათანადო უჯრაში, უნდა შეიტანოს სათანადო სიმბოლო — X (ჯვარი).
რას ვხედავთ აქ, რა სიდიდეებია? ეს არის გარკვეული გამოსახულებები, აქეთ კი — გარკვეული სიდიდეები. ცხადია, ეს გამოსახულებები უნდა გარდავქმნათ და რომელ სიდიდეს მივიღებთ, უნდა შევხედოთ. გამოიყენებთ ნიუტონის კანონს პირველ გამოსახულებაში — ძალა არის მასისა და აჩქარების ნამრავლის ტოლი; წრეზე ბრუნვის დროს, აჩქარება არის სიჩქარის კვადრატი გაყოფილი რადიუსზე, ძალა გამოვიდა — mv კვადრატი გაყოფილი R-ზე. ამ გამოსახულებას შეიტანთ პირველში და რას მიიღებთ? გამოგივიდათ მასა — m. შეხედავთ, აბა, სად გვაქვს ეს მასა — m, რა ადგილას გვაქვს? — E, ე.ი. პირველს შეესაბამება E, ჩამოყვებით პირველს და E-ს გასწვრივ, გადაკვეთაში დასვამთ ჯვარს. ასე გააგრძელებთ ყველა დანარჩენ სიდიდეებზე ოპერაციებს.
რა ეშლებათ აბიტურიენტებს? ზოგჯერ (შეიძლება ეს შემთხვევის ბრალია ან უყურადღებობის), მაგალითად, პირველის ქვევით აღნიშნულია ორი უჯრა, შესაძლოა, სხვაგან უნდა შეეტანათ ეს ჯვარი, შეეშალათ და რატომღაც პირველ უჯრაში დასვეს ორი ჯვარი. ძალიან ადვილი მისახვედრია, როდესაც, მაგალითად, ე-ს გარდა, დასვეს გ, ანუ პირველი გამოსახულება არის მასა, მას შეესაბამება მასაც და სიჩქარეც. კარგად უნდა მიხვდეს ფიზიკის მცოდნე აბიტურიენტი, რომ ასეთი რამ არ შეიძლება მოხდეს, ეს გამოსახულება გარდაქმნით ან მასა გამოვიდოდა, ან სიჩქარე, ან არც ერთი მათგანი. ამიტომ რაღაც შეცდომაა დაშვებული, ყურადღებით იყავით, გადაამოწმეთ, ხომ არ შეგეშალათ ჯვრების შეტანა სათანადო ადგილას.
ხშირად გვაქვს ამოცანები ერთეულებთან შესაბამისობაზე, ამიტომ გაითვალისწინეთ შემდეგი: შესაბამისობის ტიპის დავალებებით ხშირად ვამოწმებთ ერთეულების ცოდნას. გირჩევთ, ივარჯიშოთ — ყველა შესწავლილი ერთეული გამოსახოთ საერთაშორისო სისტემის ძირითადი ერთეულებით. ასეთი დავალებები ხშირად არის და სწორედ ეს არის ერთ-ერთი რთული დავალება ერთეულებთან დაკავშირებით. თუ ნავარჯიშევი არ ხართ, ამ დავალებას ვერ გააკეთებთ. ამიტომ, ყველა შესწავლილი სიდიდე რამდენჯერმე გამოსახეთ ძირითადი ერთეულებით. ერთი შეცდომა, რომელიც შეიძლება მოუვიდეთ აბიტურიენტებს, არის ის, რომ ბევრს ჰგონია, რომ დენის ძალის ძირითადი ერთეული არის მუხტის ერთეული — კულონი, ამიტომ გამოსახავს კულონებით. ძირითადი ერთეული კი, ელექტრული სიდიდეებიდან, არის არა მუხტის ერთეული — კულონი, არამედ დენის ძალის ერთეული — ამპერი. ამასაც მიაქციეთ ყურადღება.
ახლა არჩევითპასუხიან პატარა ამოცანებზე გადავიდეთ (მათ შორის შედარებით რთულ ამოცანებზე) და აქაც გარკვეული რჩევები მინდა, მოგცეთ. ამ ამოცანებში არის რთული დავალებებიც და მარტივი დავალებებიც. აი, მაგალითად, ერთი ასეთი დავალება:
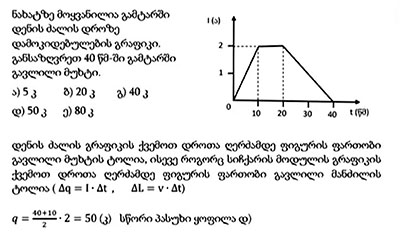 მოყვანილია დენის ძალის დროზე დამოკიდებულების გრაფიკი. დენი ცვლადია — ჯერ იზრდება, მერე გარკვეული დროის განმავლობაში მუდმივია, შემდეგ მცირდება და მთელ დროში, 40 წმ-ში, გავლილი მუხტი აინტერესებთ. როდესაც დენის ძალა მუდმივია და რაღაც დროში გავლილს გეკითხებიან, ადვილია — გაამრავლებ დენის ძალას დროზე და ადვილად იპოვი გავლილ მუხტს, მაგრამ რა ხდება, როდესაც დენის ძალა ცვლადია, რა ვქნათ? გავიხსენოთ, სად გვხვდება ანალოგიური სიტუაცია — იქ, სადაც სიჩქარე დროზეა დამოკიდებული, სიჩქარე ცვლადია, მოყვანილია სიჩქარის გრაფიკი და გარკვეულ დროში გავლილ მანძილს ეკითხებიან. როგორ ვიქცევით? სიჩქარის გრაფიკის ქვევით, დროთა ღერძის შესაბამის მონაკვეთამდე, მოქცეული ფიგურის ფართობი, რიცხობრივად, სწორედ გავლილი მანძილის ტოლი გამოდის. აქ არის ზუსტი ანალოგია, მუხტი იპოვება დენის ძალისა და დროის გამრავლებით, ანუ სიჩქარის ანალოგი დენის ძალაა, მუხტის ანალოგი — მანძილი. ამიტომ, ადვილი მისახვედრია, რომ ამ შემთხვევაში მუხტი იქნება ტრაპეციის ფართობი, რომელიც მოქცეულია დენის ძალის გრაფიკსა და დროთა ღერძს შორის და უცებ ვიანგარიშებთ. სხვა გზითაც შეიძლება ამ ამოცანის ამოხსნა, პირველ 10 წამში გავლილი მანძილი ცალკე ვიპოვოთ, შემდეგ 10 წამში — ცალკე, მაგრამ პირველ 10 წამში, რადგან დენი თანდათან მატულობს, საშუალო არითმეტიკულით ვისარგებლოთ… მაგრამ მე უფრო მოკლე გზას გეუბნებით. ეცადეთ, უფრო მოკლე გზით ამოხსნათ, ამით დროს დაზოგავთ.
მოყვანილია დენის ძალის დროზე დამოკიდებულების გრაფიკი. დენი ცვლადია — ჯერ იზრდება, მერე გარკვეული დროის განმავლობაში მუდმივია, შემდეგ მცირდება და მთელ დროში, 40 წმ-ში, გავლილი მუხტი აინტერესებთ. როდესაც დენის ძალა მუდმივია და რაღაც დროში გავლილს გეკითხებიან, ადვილია — გაამრავლებ დენის ძალას დროზე და ადვილად იპოვი გავლილ მუხტს, მაგრამ რა ხდება, როდესაც დენის ძალა ცვლადია, რა ვქნათ? გავიხსენოთ, სად გვხვდება ანალოგიური სიტუაცია — იქ, სადაც სიჩქარე დროზეა დამოკიდებული, სიჩქარე ცვლადია, მოყვანილია სიჩქარის გრაფიკი და გარკვეულ დროში გავლილ მანძილს ეკითხებიან. როგორ ვიქცევით? სიჩქარის გრაფიკის ქვევით, დროთა ღერძის შესაბამის მონაკვეთამდე, მოქცეული ფიგურის ფართობი, რიცხობრივად, სწორედ გავლილი მანძილის ტოლი გამოდის. აქ არის ზუსტი ანალოგია, მუხტი იპოვება დენის ძალისა და დროის გამრავლებით, ანუ სიჩქარის ანალოგი დენის ძალაა, მუხტის ანალოგი — მანძილი. ამიტომ, ადვილი მისახვედრია, რომ ამ შემთხვევაში მუხტი იქნება ტრაპეციის ფართობი, რომელიც მოქცეულია დენის ძალის გრაფიკსა და დროთა ღერძს შორის და უცებ ვიანგარიშებთ. სხვა გზითაც შეიძლება ამ ამოცანის ამოხსნა, პირველ 10 წამში გავლილი მანძილი ცალკე ვიპოვოთ, შემდეგ 10 წამში — ცალკე, მაგრამ პირველ 10 წამში, რადგან დენი თანდათან მატულობს, საშუალო არითმეტიკულით ვისარგებლოთ… მაგრამ მე უფრო მოკლე გზას გეუბნებით. ეცადეთ, უფრო მოკლე გზით ამოხსნათ, ამით დროს დაზოგავთ.
ახლა ცოტა რთულად გამოსათვლელი ამოცანა. პირველ ამოცანას, პასუხის გასაცემად, ბევრი გამოთვლა არ სჭირდებოდა, ამას ცოტა მეტი სჭირდება, მაგრამ არც თუ ისე რთული. ვიცით მუხტის პოტენციალი ერთ წერტილში და მეორე წერტილშიც, ვიცით, რომ b წერტილში 40%-ით მეტია პოტენციალი, ვიდრე a წერტილში. უნდა ვნახოთ, რამდენი პროცენტით მეტია დაძაბულობა b-ში, a-სთან შედარებით. ჩამოთვლილია სხვადასხვა პასუხები. გასაგებია, რომ დაძაბულობის ცვლილება პოტენციალის ცვლილებასთან უნდა დავაკავშიროთ. ყველაზე მარტივია, გავიხსენოთ მისი ფორმულები — ვიხსენებთ წერტილოვანი მუხტის შემქმნელი ველის პოტენციალის ფორმულებს, ასევე დაძაბულობის ფორმულებს. 40%-ით გაზრდის ყველაზე მარტივი ჩაწერაა — თუ სიდიდე 40%-ით გაიზარდა, ის გახდა 140%, ე.ი. ახალი პოტენციალია 1,4 გამრავლებული ძველ პოტენციალზე, ანუ პოტენციალების შეფარდება 1,4-ია. ახლა ჩვენი დაწერილი ფორმულებიდან, დაძაბულობების შეფარდება არის მანძილების კვადრატების შეფარდების ტოლი, ხოლო პოტენციალების შეფარდება მანძილების შეფარდების ტოლია. აქედან გამოდის, რომ დაძაბულობების შეფარდება ძალიან მარტივად ჩანს, ეს არის პოტენციალების შეფარდების კვადრატი, ე.ი. 1,4 რომ ავა კვადრატში, გამოვა 1,96. რას ნიშნავს ეს? ეს ნიშნავს, რომ დაძაბულობა გახდა 196%, ანუ რამდენი პროცენტით გაზრდილა? 96%-ით. ვნახოთ, სად არის ასეთი პასუხი, პასუხებს შორის, ეს არის ე). ამგვარად, მეოთხე დავალების სწორი პასუხია ე), შესაბამისად, ასე შევავსებთ სათანადო უჯრას.
 მარტივი ამოცანა ოპტიკიდან, რომელსაც არაფრის დაწერა არ სჭირდება. გაქვთ შემკრები ლინზა, ასევე გარკვეული მნათი წერტილი და აბა, ჩამოთვლილთაგან (1, 2, 3, 4, 5 წერტილი), რომელია ამის გამოსახულება? როდესაც გამოცდებისთვის ემზადებით და იხსენებთ თქვენს შესწავლილ მასალას, უნდა ააგოთ შემკრებ ლინზაში საგნის გამოსახულებები, გამვლელ ლინზაში სხვადასხვა შემთხვევები სხვადასხვა მდებარეობებში და მეტ-ნაკლებად დაგამახსოვრდებათ, მაგალითად, რომ A წერტილში მოთავსებული მნათი წერტილი არის ფოკუსსა და ორმაგ ფოკუსს შორის შემკრები ლინზის წინ. ამ შემთხვევაში, ლინზის მეორე მხარეს, ორმაგ ფოკუსს გარეთ, მიიღება გამოსახულება. თუ ეს გახსოვთ, ასეთი მხოლოდ წერტილი 5-ია და პასუხს უცებ, ყოველგვარი გამოანგარიშების გარეშე, გასცემთ.
მარტივი ამოცანა ოპტიკიდან, რომელსაც არაფრის დაწერა არ სჭირდება. გაქვთ შემკრები ლინზა, ასევე გარკვეული მნათი წერტილი და აბა, ჩამოთვლილთაგან (1, 2, 3, 4, 5 წერტილი), რომელია ამის გამოსახულება? როდესაც გამოცდებისთვის ემზადებით და იხსენებთ თქვენს შესწავლილ მასალას, უნდა ააგოთ შემკრებ ლინზაში საგნის გამოსახულებები, გამვლელ ლინზაში სხვადასხვა შემთხვევები სხვადასხვა მდებარეობებში და მეტ-ნაკლებად დაგამახსოვრდებათ, მაგალითად, რომ A წერტილში მოთავსებული მნათი წერტილი არის ფოკუსსა და ორმაგ ფოკუსს შორის შემკრები ლინზის წინ. ამ შემთხვევაში, ლინზის მეორე მხარეს, ორმაგ ფოკუსს გარეთ, მიიღება გამოსახულება. თუ ეს გახსოვთ, ასეთი მხოლოდ წერტილი 5-ია და პასუხს უცებ, ყოველგვარი გამოანგარიშების გარეშე, გასცემთ.
თუ ეს რა გახსოვთ, მაშინ შეგიძლიათ გაავლოთ სხივები, რომელთა სვლა ალბათ უნდა გახსოვდეთ, მაგალითად, A წერტილიდან გაატარებთ ცენტრზე გამავალ სხივს. თვალთახედვითაც შეგიძლიათ ეს გააკეთოთ ან, უბრალოდ, კალამი, რომლითაც მუშაობთ, მიადოთ A წერტილზე ისე, რომ ცენტრსაც გაყვეს და ნახოთ, რომელ წერტილზე გაივლის ეს სხივი. აღმოჩნდება, რომ 2-სა და 5-ზე გაივლის, შეიძლება 3-ზეც. აქ სავარაუდო წერტილი ბევრია, ე.ი. ეს სხივი არ გამოგვადგა, აბა, მოვსინჯოთ მეორე სხივი, ლინზის პარალელურად გავლილი. როგორ აგრძელებს გზას? მომდევნო ფოკუსში გადის. თუ ამ ლინზის პარალელურად გავლილ სხივს გავაყოლებთ ლინზაში მოხვედრის ადგილიდან ფოკუსზე და გავაგრძელებთ, აღმოჩნდება (ეს თვალითაც კარგად ჩანს), რომ ის წერტილ 5-ში გაივლის, ე.ი. თუ ამ სხივს გამოვიყენებთ, აქედანაც, პირდაპირ, პასუხი გამოდის, რომ არის 5.
ვთქვათ, ამ სხივის გზაზეც იყო ორი წერტილი, მაშინ რა ვქნათ? მაშინ უკვე სტანდარტული გზა რჩება — ორივე სხივი უნდა გამოვიყენოთ, ცენტრზე გამავალიც და მთავარი ოპტიკური ღერძის პარალელურიც, რომელიც, გარდატეხის შემდეგ, ვიცით, რომ გაივლის ფოკუსზე. ამ სხივების გადაკვეთით ვიპოვით მე-5 წერტილს. ეს უფრო რთულ სიტუაციაში, მაგრამ აქ ბევრად მარტივია ამოცანის ამოხსნა.
ეს არის დიაგრამა:
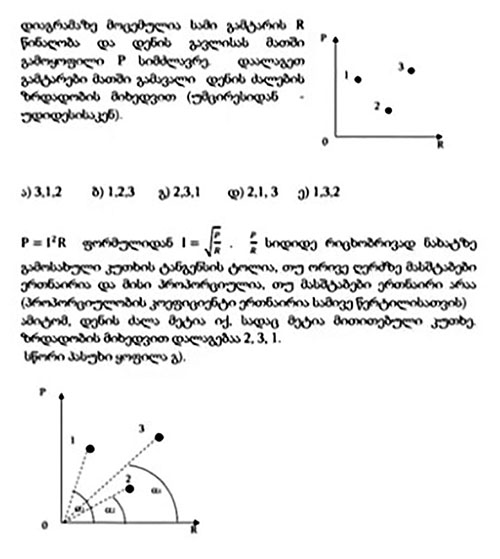 ესეც ისეთი ამოცანაა, რომელიც ძალიან მარტივად, ბევრი წვალების გარეშე შეიძლება ამოიხსნას. მოცემულია სამი სხვადასხვა გამტარი რეზისტორი, მათი წინაღობები და სიმძლავრეები; დიაგრამა სამი გამტარისთვის, მათი წინაღობები და მათში გამოყოფილი სიმძლავრეებია წარმოდგენილი და ზრდადობის მიხედვით უნდა დავალაგოთ რომელ მათგანში გადის დენის ძალები — უმცირესიდან უდიდესისკენ. ჯერ ერთი, უნდა გავიხსენოთ ფორმულა, რომ სიმძლავრე, დენის ძალით და წინაღობით, გამოისახება ფორმულით P=I2(kvadrati)R-ს და ამ ფორმულიდან დენის ძალა არის ფესვი P გაყოფილი R-დან. ე.ი. უნდა ვნახოთ, რომელი წერტილისთვის, ანუ რომელი რეზისტორისთვის არის P გაყოფილი R-ზე ყველაზე პატარა, შემდეგ — უფრო მეტი და შემდეგ — ყველაზე მეტი. რა თქმა უნდა, პირველი და მეორე ადვილად შეიძლება შეადარო — მეორეში სიმძლავრე ნაკლები გამოიყოფა და წინაღობა მეტი აქვს, ამიტომ მეორესთვის ეგ სიდიდე ნაკლებია, მაგრამ მეორე და მესამე რომ შევადარო, უფრო რთულად უნდა ვიმსჯელო — მეორე და მესამე წერტილებიდან, მესამეს, მეორესთან შედარებით, მეტი სიმძლავრე აქვს, ასევე, წინაღობაც მეტი აქვს. უნდა უყურო, რომელია აქ უფრო გაზრდილი, დავინახავთ, რომ სიმძლავრე უფრო მეტჯერაა გაზრდილი, ვიდრე წინაღობა, ამიტომ გამოდის, რომ მესამე აჯობებს მეორეს. ანალოგიურად, მერე, შეიძლება, პირველი და მესამე შევადარო, მაგრამ ეს რთული გზაა.
ესეც ისეთი ამოცანაა, რომელიც ძალიან მარტივად, ბევრი წვალების გარეშე შეიძლება ამოიხსნას. მოცემულია სამი სხვადასხვა გამტარი რეზისტორი, მათი წინაღობები და სიმძლავრეები; დიაგრამა სამი გამტარისთვის, მათი წინაღობები და მათში გამოყოფილი სიმძლავრეებია წარმოდგენილი და ზრდადობის მიხედვით უნდა დავალაგოთ რომელ მათგანში გადის დენის ძალები — უმცირესიდან უდიდესისკენ. ჯერ ერთი, უნდა გავიხსენოთ ფორმულა, რომ სიმძლავრე, დენის ძალით და წინაღობით, გამოისახება ფორმულით P=I2(kvadrati)R-ს და ამ ფორმულიდან დენის ძალა არის ფესვი P გაყოფილი R-დან. ე.ი. უნდა ვნახოთ, რომელი წერტილისთვის, ანუ რომელი რეზისტორისთვის არის P გაყოფილი R-ზე ყველაზე პატარა, შემდეგ — უფრო მეტი და შემდეგ — ყველაზე მეტი. რა თქმა უნდა, პირველი და მეორე ადვილად შეიძლება შეადარო — მეორეში სიმძლავრე ნაკლები გამოიყოფა და წინაღობა მეტი აქვს, ამიტომ მეორესთვის ეგ სიდიდე ნაკლებია, მაგრამ მეორე და მესამე რომ შევადარო, უფრო რთულად უნდა ვიმსჯელო — მეორე და მესამე წერტილებიდან, მესამეს, მეორესთან შედარებით, მეტი სიმძლავრე აქვს, ასევე, წინაღობაც მეტი აქვს. უნდა უყურო, რომელია აქ უფრო გაზრდილი, დავინახავთ, რომ სიმძლავრე უფრო მეტჯერაა გაზრდილი, ვიდრე წინაღობა, ამიტომ გამოდის, რომ მესამე აჯობებს მეორეს. ანალოგიურად, მერე, შეიძლება, პირველი და მესამე შევადარო, მაგრამ ეს რთული გზაა.
ახლა მარტივ გზას გასწავლით — თუ შევაერთებთ ამ მონაკვეთებს, პირველსა და მეორეს ცენტრთან, მივიღებთ ასეთ მონაკვეთებს, დააკვირდით. ამ კუთხის ტანგენსი არის P გაყოფილი R-ზე, გასაგებია, როცა ტოლ მასშტაბებშია ღერძებზე R და P, ანუ თითოეული ერთეული ტოლი მონაკვეთებით არის გამოსახული. თუ ტოლი მონაკვეთებით არ არის გამოსახული, უბრალოდ, ტანგეს ალფას პროპორციული იქნება P გაყოფილი R, გარკვეულ მუდმივ A-ზე გამრავლებული P გაყოფილი R იქნება ტანგეს ალფა ან P გაყოფილი R იქნება ტანგეს ალფა გამრავლებული გარკვეულ მუდმივაზე. ოღონდ ეს მუდმივა იქნება მხოლოდ მასშტაბებზე დამოკიდებული და ყველასთვის ერთნაირი იქნება. ასე რომ, კუთხეების შედარებით, ტანგეს ალფების შედარებით, მივხვდებით რომელია უფრო დიდი P გაყოფილი R და რას დავინახავთ? ყველაზე პატარა კუთხე არის მეორესთვის, შემდეგ — უფრო მეტი მესამესთვის და ყველაზე მეტი — პირველისთვის, ე.ი. ტანგეს ალფა ასე იზრდება — ჯერ მეორეს აქვს ყველაზე ნაკლები, შემდეგ მესამეს — უფრო მეტი და ყველაზე მეტი — პირველს. შესაბამისად, ყველაფერს სწორად დავალაგებთ.
აი, ასეთი მსჯელობით, მიდგომებით და ყურადღებით უნდა გააკეთოთ ეს ამოცანები და უფრო გაგიადვილდებათ. ყველაფერი იქნება კარგად, გისურვებთ წარმატებებს!






