ამირან თავაძე
მათემატიკის მასწავლებელი
სამტრედია, საჯავახოს საჯარო სკოლა
მოგეხსენებათ, ზუსტი მეცნიერებები სწავლების თანამედროვე მიდგომების აქილევსის ქუსლია. ხშირად გსმენიათ, რომ ცალკეულ საკითხებს არგებენ ხოლმე სხვადასხვა მეთოდებს, მაგრამ, როცა საქმე მათემატიკურ სიღრმეებთან მიდის, მაშინ მხოლოდ რუტინული შრომა, ნიჭიერება და შესაძლებლობების მაქსიმალური გამოყენებაა აუცილებელი.
მოსწავლეებში მათემატიკისადმი ინტერესის გაღვივების და მოტივაციის ამაღლების მიზნით, ხშირად ვიყენებ სახალისო ამოცანებს, რაც მათ ძალიან მოსწონთ. ერთ-ერთ შემთხვევაში წამოიჭრა საკითხი,თუ როგორ დაგვეთვალა კვადრატები მარტივად, სადაც ერთი ,,დიდი’’ კვადრატი იყო დაყოფილი, ვთქვათ, k∙k რაოდენობის კვადრატებად (იგულისხმება დასათვლელად ყველა (ზომის) კვადრატი). გარკვეული პერიოდის შემდეგ გამოვიყვანე ეს ფორმულა, ![]() რომლის შესახებ ჩემი მოსაზრება გავანდე ერთ- ერთ პროფესორსა და სახელმძღვანელოს ავტორს. მან მითხრა, რომ ეს უკვე დამტკიცებული იყო და გამომიგზავნა კიდეც საკმაოდ რთული გზით დამტკიცება, რაც საშუალო საფეხურის მყოფი მოზარდებისთვის არ აღმოჩნდა მარტივი.
რომლის შესახებ ჩემი მოსაზრება გავანდე ერთ- ერთ პროფესორსა და სახელმძღვანელოს ავტორს. მან მითხრა, რომ ეს უკვე დამტკიცებული იყო და გამომიგზავნა კიდეც საკმაოდ რთული გზით დამტკიცება, რაც საშუალო საფეხურის მყოფი მოზარდებისთვის არ აღმოჩნდა მარტივი.
გამუდმებული ფიქრის შემდეგ მივაგენი მარტივ ხერხს, რომელიც გადავწყვიტე თქვენთვის გამეზიარებინა. მათემატიკის მოყვარულებს და არა მარტო მათ, ვთავაზობ ერთ-ერთ მათემატიკურ მიგნებას, პასუხს კითხვაზე – ,,რამდენი კვადრატია?“
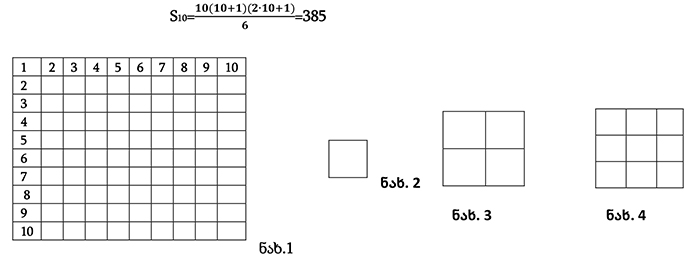
განვიხილოთ რაიმე ზომის კვადრატი და დავყოთ ის, როგორც ნახაზზეა ნაჩვენები, 100 მცირე ზომის ტოლ კვადრატად (ნახ.1). დავსვათ კითხვა: სულ რამდენი კვადრატია? (სხვადასხვა ზომის). ცხადია, ძალიან რთულია უშუალოდ დათვლა. არსებობს თუ არა რაიმე ფორმულა ყველა კვადრატის დასათვლელად? მივყვეთ ნაბიჯ-ნაბიჯ. განვიხილოთ შემთხვევები, როდესაც კვადრატებად დაყოფა არ გამოისახება დიდი რიცხვით, როდესაც შეგვიძლია დავთვალოთ უშუალოდ ყველა კვადრატის რაოდენობა. 1 კვადრატი (ნახ.2). 5 კვადრატი (ნახ.3).14 კვადრატი (ნახ.4).
ეს რიცხვები ასე წარმოვადგინოთ:
1=12; 5=12+22; 14=12+22+32; 30=12+22+32+42 და ა.შ. ანუ კვადრატების რაოდენობა იზრდება იმ რიცხვის კვადრატით, რომელიც წარმოადგენს ერთ გვერდთან მდებარე ყველაზე მცირე კვადრატების რაოდენობას.
ახლა დავამტკიცოთ, რომ ამ კანონზომიერების განზოგადება შეიძლება, ანუ თუ გარკვეული ზომის კვადრატს დავყოფთ რაიმე ზომის ტოლ კვადრატებად, ისე რომ თავდაპირველი კვადრატის ერთ გვერდთან მდებარე ყველაზე მცირე კვადრატების რაოდენობაა k (ნახ.5), მაშინ ყველა კვადრატის რაოდენობა (აღვნიშნოთ ის SK-თი) გამოითვლება ფორმულით: SK =12+22+32+…+k 2
დავამტკიცოთ მათემატიკური ინდუქციის მეთოდით.
- როცა k=1 გვაქვს S1 =12=1 ჭეშმარიტია
- დავუშვათ, რომ სამართლიანია Sk =12+22+32+…+k2 ფორმულა და დავამტკიცოთ დაშვების საფუძველზე, რომ
- Sk+1=12+22+32+…+k2+(k+1)2
ამ უკანასკნელ კვადრატში (ნახ.6) გადანომრილია წინა კვადრატს ,,მიერთებული“ ,,ახალი“ მცირე კვადრატები. დავითვალოთ რამდენი კვადრატი ,,წარმოიქმნა“ მათ მიერ და დავუმატოთ ის SK-ს,რომელიც დაშვების თანახმად (12+22+32+…+k2)-ის ტოლია.
1-ლი კვადრატი შედის k+1 რაოდენობის კვადრატში, მე-2კვადრატი შედის k რაოდენობის კვადრატში
…
(k+1)-ე კვადრატი 1 ცალი
(k+2)-ე კვადრატი შედის k რაოდენობის კვადრატში
…
(2k+1)-ე კვადრატი 1 ცალი
შევნიშნოთ, რომ, მაგალითად, (k+2)-ე კვადრატი შედის უფრო მეტ კვადრატში, მაგრამ ისინი ზემოთ ათვლილი გვაქვს. შევკრიბოთ ეს რაოდენობები:
(k+1)+k+(k-1)+…+1+k+(k -1)+…+1=k+1+2(1+2+…+k)=k+1+(k+1)k=(k+1)2
ეს რაოდენობა დავუმატოთ Sk-ს, მივიღებთ Sk+1-ის ფორმულას:
Sk+1=Sk+(k+1)2=12+22+32+…+k2+(k+1)2 ე.ი. დამტკიცდა (k+1)-სთვისაც, საბოლოოდ გვაქვს:
Sk=12+22+32+…+k2
ცნობილია, რომ ![]()
ესეც მათემატიკური ინდუქციით მტკიცდება ამის გათვალისწინებით
![]()
ახლა შეგვიძლია დასაწყისში მოცემულ ნახაზზე გამოვთვალოთ ყველა კვადრატის რაოდენობა: