ზაზა თევდორაძე – შეფასებისა და გამოცდების ეროვნული ცენტრის მათემატიკის ჯგუფის ხელმძღვანელი
დღეს მინდა, გესაუბროთ მათემატიკის ტესტის სტრუქტურაზე, ასევე, გასულ წლებში, აბიტურიენტების მიერ დაშვებულ შეცდომებზე და მოგცეთ რჩევები, რომელიც, ვიმედოვნებ, დაგეხმარებათ, უკეთ შეასრულოთ მათემატიკის ტესტი. 2021 წლის ეროვნული გამოცდის მათემატიკის ტესტის სტრუქტურამ მცირე ცვლილება განიცადა. თავიდანვე ვიტყვი, რომ ცვლილება არ შეხებია საგამოცდო პროგრამას, რომლის ნახვა თქვენ შეგიძლიათ გამოცდების ეროვნული ცენტრის ვებგვერდზე. იქ წარმოდგენილია, ასევე, კრებულები, ერთ-ერთია „როგორ მოვემზადოთ ერთიანი ეროვნული გამოცდისათვის მათემატიკაში 2021 წელს“, სადაც თქვენ შეგიძლიათ იხილოთ საგამოცდო პროგრამა, ნახოთ როგორი იყო ძველი დავალებები, როგორ სწორდება ეს დავალებები, აგრეთვე, აბიტურიენტების მიერ, გასულ წლებში, დაშვებული ხარვეზები და რჩევები, როგორ ავირიდოთ თავიდან ეს ხარვეზები.
განვიხილოთ ახალი ტესტის სტრუქტურა. წლევანდელი ტესტი შედგება 35 დავალებისგან, აქედან პირველი 27 ე.წ. არჩევითპასუხებიანი დავალებაა, თითოეულ მათგანს ახლავს 4 სავარაუდო პასუხი, რომელთაგან მხოლოდ ერთია სწორი. თქვენი ნაშრომი შეფასდება 1 ქულით, თუ თქვენ პასუხების ფურცელზე გადაიტანთ ამ სწორი პასუხის შესაბამის აღმნიშვნელ ასოს, ჯვრით, მაგალითად, ა), ან ბ), ან გ), ან დ). ტესტის დანარჩენი დავალებები, 28-დან 35-ის ჩათვლით, წერითი დავალებებია, აქედან პირველი ორი 2-ქულიანია, შემდეგი 4 – 3-ქულიანი, ბოლო 2 დავალება 4-ქულიანია.
წერითი დავალების შეფასება განსხვავებული წესით ხდება. ინსტრუქციაში, რომელიც ტესტს თან ახლავს, წაიკითხავთ მოთხოვნას წერითი დავალებების შესახებ. იქ თვალნათლივ და ერთმნიშვნელოვნადაა აღნიშნული, რომ წერითი დავალების პასუხი ჩაწერილი და წარმოდგენილი უნდა იყოს მწყობრი ლოგიკური გადასვლებით, ყველა დეტალი უნდა იყოს აღნიშნული. თუ თქვენ, მაგალითად, ზეპირად დაწერთ პასუხს და არ იქნება ნაჩვენები ამ პასუხის მიღების გზა, მაშინ ეს დავალება დადებითი ქულით არ შეფასდება. წერითი დავალება ფასდება შემდეგი სტრუქტურის მიხედვით, მაგალითად, დავალება 4-ქულიანია, ეს არ ნიშნავს იმას, რომ თქვენ მიიღებთ მხოლოდ 4 ქულას, თუ გააკეთებთ ან მიიღებთ 0 ქულას, თუ ვერ გააკეთებთ. თქვენი ნაშრომი შეიძლება შეფასდეს ნებისმიერი შუალედური მთელი რიცხვით, მაგალითად, შეფასდეს 1 ქულით, 2 ქულით, 3 ქულით, ასევე 4-ით ან 0 ქულით.
განვიხილოთ, რის მიხედვით ვიღებთ ჩვენ ამა თუ იმ შეფასებას. თითოეული წერითი დავალების ამოხსნა დაყოფილია ეტაპებად. ეტაპი რისგან შედგება? ეტაპი შედგება ამ ამოცანის ამოხსნისათვის საჭირო რაიმე სიდიდის პოვნისგან და ასევე, საჭირო სიდიდეებს შორის კავშირის დადგენისგან. გიჩვენებთ ასეთი შეფასების სქემის ერთ-ერთ ნიმუშს, რომ წარმოდგენა შეგვექმნას, რაზეა საუბარი.
 ეს არის გასული წლის ერთ-ერთი ვარიანტის (გასულ წელს, მოგეხსენებათ, ორი ვარიანტი იყო) 31-ე დავალება. ამ დავალების შეფასების სქემა ეგზავნება გამსწორებლებს და ისინი, მასზე დაყრდნობით, აფასებენ თქვენს ნამუშევარს. რას ვხედავთ ამ შეფასების სქემაში? 31-ე დავალება ითხოვს, ვიპოვოთ წარმოდგენილი უტოლობათა სისტემის ამონახსნთა სიმრავლე, მოკლედ რომ ვთქვათ, ამოვხსნათ უტოლობათა სისტემა. მოცემულია ამოხსნის ერთ-ერთი ვარიანტი. უფრო რთულ დავალებას, შესაძლოა, ამოხსნის რამდენიმე ვარიანტიც კი ჰქონდეს – 2, 3 ან 4 ვარიანტიც კი მოიძებნოს. ამის შემდეგ, მოდის ამოხსნის ეტაპები. მე სპეციალურად შევარჩიე ყველაზე მარტივი დავალება, სწრაფად რომ გავიაროთ და უბრალოდ, პრინციპულად გავიგოთ, როგორ ხდება თქვენი ნაშრომის შეფასება (რთული დავალება არ გვინდა, რადგან დიდ დროს მოითხოვს განსახილველად). როგორც ვხედავთ, აქ ორი ეტაპია — პირველი ეტაპი ა) პუნქტითაა აღნიშნული და გვეუბნება, რომ აბიტურიენტმა იპოვა სისტემაში შემავალი ერთ-ერთი უტოლობის ამონახსნი, უფრო სწორად რომ ვთქვათ, ამონახსნთა სიმრავლე, ხოლო ბ) პუნქტი ამბობს, რომ იპოვა თავად სისტემის ამონახსნთა სიმრავლე. გამსწორებელი რომ ხედავს ამ შეფასების სქემას, მისთვის უკვე ძალიან მარტივია ქულების დაწერა. შეიძლება, მაგალითად, სისტემაში შემავალი ორივე უტოლობა ამოხსნათ, მაგრამ შეფასების სქემა ცალსახად ამბობს, რომ მაინც იწერება ერთი ქულა იმიტომ, რომ ორივე უტოლობის ამოხსნა ჯერ კიდევ არ ნიშნავს სისტემის ამოხსნას, შემდეგ უნდა იპოვოთ ამ ამონახსნთა სიმრავლეების თანაკვეთა.
ეს არის გასული წლის ერთ-ერთი ვარიანტის (გასულ წელს, მოგეხსენებათ, ორი ვარიანტი იყო) 31-ე დავალება. ამ დავალების შეფასების სქემა ეგზავნება გამსწორებლებს და ისინი, მასზე დაყრდნობით, აფასებენ თქვენს ნამუშევარს. რას ვხედავთ ამ შეფასების სქემაში? 31-ე დავალება ითხოვს, ვიპოვოთ წარმოდგენილი უტოლობათა სისტემის ამონახსნთა სიმრავლე, მოკლედ რომ ვთქვათ, ამოვხსნათ უტოლობათა სისტემა. მოცემულია ამოხსნის ერთ-ერთი ვარიანტი. უფრო რთულ დავალებას, შესაძლოა, ამოხსნის რამდენიმე ვარიანტიც კი ჰქონდეს – 2, 3 ან 4 ვარიანტიც კი მოიძებნოს. ამის შემდეგ, მოდის ამოხსნის ეტაპები. მე სპეციალურად შევარჩიე ყველაზე მარტივი დავალება, სწრაფად რომ გავიაროთ და უბრალოდ, პრინციპულად გავიგოთ, როგორ ხდება თქვენი ნაშრომის შეფასება (რთული დავალება არ გვინდა, რადგან დიდ დროს მოითხოვს განსახილველად). როგორც ვხედავთ, აქ ორი ეტაპია — პირველი ეტაპი ა) პუნქტითაა აღნიშნული და გვეუბნება, რომ აბიტურიენტმა იპოვა სისტემაში შემავალი ერთ-ერთი უტოლობის ამონახსნი, უფრო სწორად რომ ვთქვათ, ამონახსნთა სიმრავლე, ხოლო ბ) პუნქტი ამბობს, რომ იპოვა თავად სისტემის ამონახსნთა სიმრავლე. გამსწორებელი რომ ხედავს ამ შეფასების სქემას, მისთვის უკვე ძალიან მარტივია ქულების დაწერა. შეიძლება, მაგალითად, სისტემაში შემავალი ორივე უტოლობა ამოხსნათ, მაგრამ შეფასების სქემა ცალსახად ამბობს, რომ მაინც იწერება ერთი ქულა იმიტომ, რომ ორივე უტოლობის ამოხსნა ჯერ კიდევ არ ნიშნავს სისტემის ამოხსნას, შემდეგ უნდა იპოვოთ ამ ამონახსნთა სიმრავლეების თანაკვეთა.
ახლა მინდა წარმოგიდგინოთ, როგორც დაგპირდით, გასულ წლებში აბიტურიენტთა ნაშრომებში შემჩნეული ხარვეზები, რომელიც წლიდან წლამდე მეორდება და აქვე, მოკრძალებულად, მოგცეთ გარკვეული რჩევები, რომელიც, ვიმედოვნებ, დაგეხმარებათ, უკეთ შეასრულოთ მათემატიკის ტესტი.
პირველ, რიგში, ყურადღებით წავიკითხოთ ამოცანა, კარგად გავიაზროთ მასში მოცემული პირობები, ამოცანის ამოხსნა პასუხების ფურცელზე დავწეროთ ზუსტად ამ ამოცანის პასუხისათვის გამოყოფილ ადგილზე. რატომ გაძლევთ ასეთ რჩევას? იმიტომ, რომ გავრცელებული შეცდომაა, როდესაც აბიტურიენტი ამას არ აქცევს ყურადღებას და თუნდაც სწორად ამოხსნილ დავალებას, პასუხების ფურცელზე, სხვა დავალების ადგილას წერს, რაც იწვევს პრობლემას. რა სახის პრობლემას? მაგალითად, 28-ე ამოცანის ამოხსნა დაწერეთ 33-ე ამოცანისათვის გამოყოფილ ადგილას, ეს ნიშნავს, რომ 33-ე ამოცანის გამსწორებელს მისდის თქვენი ნაწერი და რადგან მას არ აქვს უფლება, გაასწოროს სხვა დავალება (ის მხოლოდ 33-ე დავალების გამსწორებელია), ერთადერთი გზა დარჩენია — ნაწერი გადააგზავნოს პრობლემურ დავალებებში. შემდეგ ცალკე უნდა შეიკრიბოს კომისია, დავალება ამოიბეჭდოს ფურცელზე და ქაღალდზე გასწორდეს. ეს იწვევს გამოცდის შედეგების გამოცხადების გადავადებას, ზედმეტი პრობლემაა და ამიტომ, დაბეჯითებით გთხოვთ, ყოველი დავალების პასუხი ზუსტად ამ დავალებისათვის გამოყოფილ ადგილზე გადაიტანოთ პასუხების ფურცელზე. ეს არ არის რთული საქმე – 8 ღია დავალებაა და ძალიან მარტივია, თითოეული მათგანი დააკავშიროთ ამ კონკრეტული ამოცანისთვის გამოყოფილ ადგილს პასუხების ფურცელზე.
საგამოცდო დავალების თანმხლებ ინსტრუქციაში ჩვენ, ასევე, ვკითხულობთ, რომ ღია დავალებებში, სადაც მოითხოვენ ამოცანის ამოხსნის დემონსტრირებას, აბიტურიენტის ჩანაწერში მკაფიოდ და ნათლად უნდა ჩანდეს ამოცანის ამოხსნის გზა. კიდევ განვმეორდები და გეტყვით, რომ თუ თქვენს ნაწერში არ იქნება ამოცანის ამოხსნის დემონსტრირება, თუნდაც სწორი პასუხის შემთხვევაში (მაგალითად, გეკითხებიან წრეწირის რადიუსს და დაწერთ, რომ რადიუსი უდრის 3 სანტიმეტრს), ნაშრომი არ შეფასდება დადებითი ქულით, შეფასდება 0 ქულით იმიტომ, რომ ტესტის სტრუქტურით და ინსტრუქციით, მოგეთხოვებათ, რომ აჩვენოთ თქვენი მათემატიკური უნარები, ასევე, ლოგიკური მსჯელობის უნარი და თანმიმდევრულად გამართული პასუხი გასცეთ, როგორ იმსჯელეთ, რა ფაქტებზე დაყრდნობით, რა თეორემები და ფორმულები გამოიყენეთ. ინსტრუქციის მიუხედავად, ტესტებში ძალიან ბევრი ხარვეზია აბიტურიენტების მიერ დაშვებული და ამ მაგალითებს იმიტომ გიჩვენებთ (რასაკვირველია, შესანიშნავი ნაწერებიც არის, ბრწყინვალე აბიტურიენტებიც გვყავს. სამწუხაროდ, მათი წილი არ არის იმდენი, რამდენიც სასურველია იყოს) და ვამახვილებთ ყურადღებას ხარვეზებზე, რომ ზუსტად ამ ხარვეზების ცოდნა დაგვეხმარება, უკეთ დავწეროთ ტესტი. მაგალითად, 33-ე დავალება, გეომეტრია – პლანიმეტრიის დავალება.
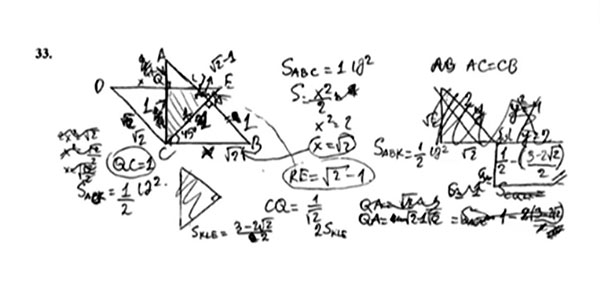 უკვე არც არის საჭირო, გავერკვეთ ამ დავალების პირობაში. თავად ხედავთ, რომ ეს დავალება თეთრად არის წარმოდგენილი იმ სახით, რომლის წაკითხვა, ფაქტობრივად, შეუძლებელია. თქვენი თავი რომ წარმოიდგინოთ გამსწორებლის ადგილას, როგორ უნდა შეაფასოთ, როგორი კეთილგანწყობილიც არ უნდა იყოთ, მსგავსი ნაწერი – ნახაზი გადახაზულია, ზედ წარწერაც გადახაზული, თავიდანაა გაკეთებული წარწერა და ისევ გადახაზულია, ტექსტებიც გადახაზული… შეგახსენებთ, რომ თქვენ გეძლევათ სავარჯიშო ფურცლები განუსაზღვრელი რაოდენობით. თუ გაგითავდებათ, შეგიძლიათ მოითხოვოთ და დამატებით ფურცლებს მოგცემენ. სავარჯიშო ფურცელი ზუსტად იმისთვისაა გამიზნული, რომ იქ თქვენი ნაშრომი რამდენჯერაც გინდათ გადახაზოთ და თავიდან დაიწყოთ ამოხსნა, მაგრამ პასუხების ფურცელში, სადაც გადაათეთრებთ, უკვე გამართული ტექსტი უნდა დაწეროთ, ისეთი ტექსტი მაინც, რომელიც წაკითხვადი იქნება. მათემატიკაში, მოგეხსენებათ, ამა თუ იმ ფორმულის გადახაზვა პრობლემა არ არის, ამისთვის თქვენ ქულა არ დაგაკლდებათ, მაგრამ იმდენი არ უნდა გადახაზოთ, რომ წაკითხვა შეუძლებელი გახდეს. ეს ორი დავალება ამის სადემონსტრაციოდ წარმოგიდგინეთ. 36-ე დავალება ტექსტური დავალებაა, ამას კიდევ არა უშავს, 33-სთან შედარებით, თუმცა, სასურველია, რომ, როდესაც გადათეთრებაზე მიდგება საქმე, უფრო აკურატულად და კარგად შეასრულოთ გადათეთრების პროცედურა.
უკვე არც არის საჭირო, გავერკვეთ ამ დავალების პირობაში. თავად ხედავთ, რომ ეს დავალება თეთრად არის წარმოდგენილი იმ სახით, რომლის წაკითხვა, ფაქტობრივად, შეუძლებელია. თქვენი თავი რომ წარმოიდგინოთ გამსწორებლის ადგილას, როგორ უნდა შეაფასოთ, როგორი კეთილგანწყობილიც არ უნდა იყოთ, მსგავსი ნაწერი – ნახაზი გადახაზულია, ზედ წარწერაც გადახაზული, თავიდანაა გაკეთებული წარწერა და ისევ გადახაზულია, ტექსტებიც გადახაზული… შეგახსენებთ, რომ თქვენ გეძლევათ სავარჯიშო ფურცლები განუსაზღვრელი რაოდენობით. თუ გაგითავდებათ, შეგიძლიათ მოითხოვოთ და დამატებით ფურცლებს მოგცემენ. სავარჯიშო ფურცელი ზუსტად იმისთვისაა გამიზნული, რომ იქ თქვენი ნაშრომი რამდენჯერაც გინდათ გადახაზოთ და თავიდან დაიწყოთ ამოხსნა, მაგრამ პასუხების ფურცელში, სადაც გადაათეთრებთ, უკვე გამართული ტექსტი უნდა დაწეროთ, ისეთი ტექსტი მაინც, რომელიც წაკითხვადი იქნება. მათემატიკაში, მოგეხსენებათ, ამა თუ იმ ფორმულის გადახაზვა პრობლემა არ არის, ამისთვის თქვენ ქულა არ დაგაკლდებათ, მაგრამ იმდენი არ უნდა გადახაზოთ, რომ წაკითხვა შეუძლებელი გახდეს. ეს ორი დავალება ამის სადემონსტრაციოდ წარმოგიდგინეთ. 36-ე დავალება ტექსტური დავალებაა, ამას კიდევ არა უშავს, 33-სთან შედარებით, თუმცა, სასურველია, რომ, როდესაც გადათეთრებაზე მიდგება საქმე, უფრო აკურატულად და კარგად შეასრულოთ გადათეთრების პროცედურა.
 განსაკუთრებული პრობლემაა ჩვენი აბიტურიენტებისთვის და ზოგადად, სკოლისთვის გეომეტრიული ნახაზების აგება (საზოგადოდ, გეომეტრია). ეს სხვადასხვა კვლევაშიც დასტურდება. ამას წინათაც ჩატარდა კვლევა და ჩვენმა მოსწავლეებმა, მათემატიკიდან, ყველაზე რთულ ნაწილად გეომეტრიული ნაწილი მიიჩნიეს. ახლა გიჩვენებთ 38-ე დავალებას:
განსაკუთრებული პრობლემაა ჩვენი აბიტურიენტებისთვის და ზოგადად, სკოლისთვის გეომეტრიული ნახაზების აგება (საზოგადოდ, გეომეტრია). ეს სხვადასხვა კვლევაშიც დასტურდება. ამას წინათაც ჩატარდა კვლევა და ჩვენმა მოსწავლეებმა, მათემატიკიდან, ყველაზე რთულ ნაწილად გეომეტრიული ნაწილი მიიჩნიეს. ახლა გიჩვენებთ 38-ე დავალებას:
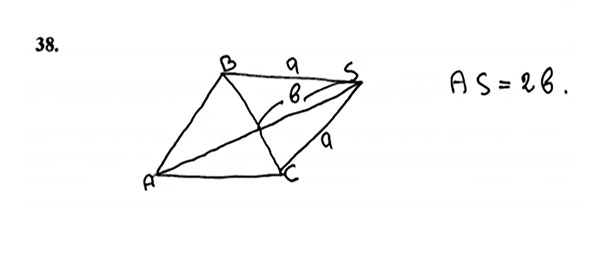 ამას მარტო გამსწორებელი კი არა, ვერავინ ვერ გაიგებს, რა არის აქ გამოსახული. აბიტურიენტს აქვს მცდელობა, გამოსახოს პირამიდა, თითქოს ეს სამკუთხა პირამიდაა, რომელიც სინამდვილეში, თუ ნახაზს დავუჯერებთ, წარმოადგენს რომბს. ძალიან დიდ პრობლემად რჩება სტერეომეტრიული ნახაზების შესრულება, უჭირთ ჩვენს აბიტურიენტებს. როგორც ჩანს, სკოლაში არ ექცევა სათანადო ყურადღება ამ მასალას, ზოგადად გეომეტრიას და შემდეგ ეს სავალალო მდგომარეობა გამოცდაზე შესრულებულ ნაშრომებში აისახება. ჩემი დაბეჯითებული თხოვნაა, როდესაც გეომეტრიულ ნახაზებს შეასრულებთ, ძალიან დაკვირვებულად და კარგად წარმოადგინოთ, ისე, რომ გამსწორებელს შეეძლოს იმის აღქმა, რისი გადმოცემა გინდოდათ ამ ნახაზით.
ამას მარტო გამსწორებელი კი არა, ვერავინ ვერ გაიგებს, რა არის აქ გამოსახული. აბიტურიენტს აქვს მცდელობა, გამოსახოს პირამიდა, თითქოს ეს სამკუთხა პირამიდაა, რომელიც სინამდვილეში, თუ ნახაზს დავუჯერებთ, წარმოადგენს რომბს. ძალიან დიდ პრობლემად რჩება სტერეომეტრიული ნახაზების შესრულება, უჭირთ ჩვენს აბიტურიენტებს. როგორც ჩანს, სკოლაში არ ექცევა სათანადო ყურადღება ამ მასალას, ზოგადად გეომეტრიას და შემდეგ ეს სავალალო მდგომარეობა გამოცდაზე შესრულებულ ნაშრომებში აისახება. ჩემი დაბეჯითებული თხოვნაა, როდესაც გეომეტრიულ ნახაზებს შეასრულებთ, ძალიან დაკვირვებულად და კარგად წარმოადგინოთ, ისე, რომ გამსწორებელს შეეძლოს იმის აღქმა, რისი გადმოცემა გინდოდათ ამ ნახაზით.
აი, შემდეგი ორი დავალება, ასევე სტერეომეტრიიდან (გეომეტრიიდან). აქ რა ხარვეზია? აბიტურიენტები არ აანალიზებენ ამოცანის პირობას.
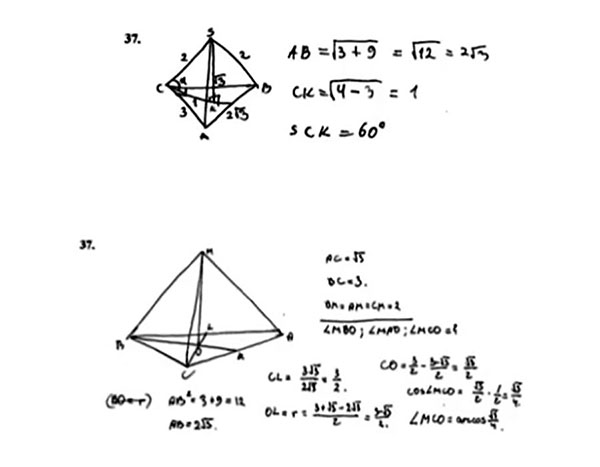 პირამიდა თითქოს შედარებით კარგად ხატია, გარჩევადია, მაგრამ ამ ამოცანის ტექსტი შემდეგი იყო — სამკუთხა პირამიდის ფუძე არის მართკუთხა სამკუთხედი, რომლის კათეტები არის მოცემული 3 და კვადრატული ფესვი 3-დან, ასევე, ცნობილია ამ ამოცანაში, რომ პირამიდის ყველა გვერდითი წიბო ერთმანეთის ტოლია და უდრის 2 სანტიმეტრს. ამოცანა გვავალებს, ვიპოვოთ ამ პირამიდის წიბოების მიერ ფუძის სიბრტყესთან შედგენილი კუთხე. აქ ორი ნაწერია წარმოდგენილი, ერთმანეთის ქვემოთ. ვხედავთ, რომ პირამიდის წვერო, ავტომატურად, დააგეგმილეს პირამიდის ფუძის შიგნით, შუა წერტილში, სადღაც, მაშინ როდესაც, კარგად რომ გაეანალიზებინათ ეს ტექსტი და ამოცანის პირობა, შეამჩნევდნენ, რომ პირამიდის წვერო, ამ პირობებში, გეგმილდება ფუძეზე შემოხაზული წრეწირის ცენტრში. რადგან ფუძეში მართკუთხა სამკუთხედია, მასზე შემოხაზული წრეწირი, რასაკვირველია, ჰიპოტენუზის შუა წერტილში მდებარეობს და სწორედ ამან გამოიწვია ის ხარვეზები, რომელიც ამოხსნაშია დაშვებული. პირველ ამოცანაში, რომელიც უფრო ზემოთ არის განთავსებული, ჩაწერის პრობლემაცაა — აბიტურიენტმა დააწერა, რომ კათეტი CD არის კვადრატული ფესვი 3-დან, როგორც ტექსტშია მოცემული, მაგრამ შემდეგ, რადგან SK პირამიდის სიმაღლესთან ახლოს მდებარეობს, უცებ ჩათვალა, რომ SK-ს ტოლია, ანუ რადგან ჩაწერა არ იყო აკურატული და კარგად გაფორმებული, ამან შემდეგი შეცდომაც გამოიწვია.
პირამიდა თითქოს შედარებით კარგად ხატია, გარჩევადია, მაგრამ ამ ამოცანის ტექსტი შემდეგი იყო — სამკუთხა პირამიდის ფუძე არის მართკუთხა სამკუთხედი, რომლის კათეტები არის მოცემული 3 და კვადრატული ფესვი 3-დან, ასევე, ცნობილია ამ ამოცანაში, რომ პირამიდის ყველა გვერდითი წიბო ერთმანეთის ტოლია და უდრის 2 სანტიმეტრს. ამოცანა გვავალებს, ვიპოვოთ ამ პირამიდის წიბოების მიერ ფუძის სიბრტყესთან შედგენილი კუთხე. აქ ორი ნაწერია წარმოდგენილი, ერთმანეთის ქვემოთ. ვხედავთ, რომ პირამიდის წვერო, ავტომატურად, დააგეგმილეს პირამიდის ფუძის შიგნით, შუა წერტილში, სადღაც, მაშინ როდესაც, კარგად რომ გაეანალიზებინათ ეს ტექსტი და ამოცანის პირობა, შეამჩნევდნენ, რომ პირამიდის წვერო, ამ პირობებში, გეგმილდება ფუძეზე შემოხაზული წრეწირის ცენტრში. რადგან ფუძეში მართკუთხა სამკუთხედია, მასზე შემოხაზული წრეწირი, რასაკვირველია, ჰიპოტენუზის შუა წერტილში მდებარეობს და სწორედ ამან გამოიწვია ის ხარვეზები, რომელიც ამოხსნაშია დაშვებული. პირველ ამოცანაში, რომელიც უფრო ზემოთ არის განთავსებული, ჩაწერის პრობლემაცაა — აბიტურიენტმა დააწერა, რომ კათეტი CD არის კვადრატული ფესვი 3-დან, როგორც ტექსტშია მოცემული, მაგრამ შემდეგ, რადგან SK პირამიდის სიმაღლესთან ახლოს მდებარეობს, უცებ ჩათვალა, რომ SK-ს ტოლია, ანუ რადგან ჩაწერა არ იყო აკურატული და კარგად გაფორმებული, ამან შემდეგი შეცდომაც გამოიწვია.
ჩვენი რჩევა ასეთია, სტერეომეტრიული ნახაზები ააგეთ აკურატულად, წინასწარ მოიფიქრეთ ნახაზის დეტალები, მაგალითად, სად ეცემა ამ დროს პირამიდის სიმაღლე – პირამიდის ფუძის შიგნით, პირამიდის ფუძეზე შემოხაზული წრეწირის ცენტრში თუ ფუძეში ჩახაზული წრეწირის ცენტრში ან რომელიმე სხვა წერტილში. ზოგჯერ, ამოცანის ამოხსნისას, გამოტოვებულია ამოხსნის გარკვეული ეტაპი და, ყოველგვარი დასაბუთების გარეშე, მითითებულია საძიებელი ან შუალედური სიდიდის მნიშვნელობა. ამის სადემონსტრაციოდ აქ კიდევ ორი ამოცანაა წარმოდგენილი.
 მაგალითად, პირველ ამოცანაში, №37, აბიტურიენტს მოცემული აქვს წრფე, წრფის განტოლება, მან ეს მოცემულობაში ჩაწერა და ეს წრფე ეხება წრის სექტორს, რომლის ცენტრი მდებარეობს კოორდინატთა სისტემის სათავეში, უნდა ეპოვა წრის რადიუსი. ყოველგვარი დასაბუთების გარეშე, დაწერა, რომ რადიუსი არის 3 ერთეულის ტოლი. სინამდვილეში, ეს ამოცანა რომ ამოვხსნათ, რადიუსი მართლაც 3 ერთეულის ტოლია და მან, სავარაუდოდ, ეს სავარჯიშო ფურცელზე შეასრულა, მაგრამ არ გადმოიტანა თეთრ ფურცელზე. ამ დროს, ჩვენ უნდა ვიცოდეთ, მეგობრებო, რა გზით მიხვედით პასუხამდე. სავარჯიშო ფურცლები გამსწორებლებს არ მისდის, ეს მხოლოდ თქვენთვის არის გამოყოფილი, რომ ამოცანის ამოსახსნელად სხვადასხვა გზა მოსინჯოთ და მხოლოდ ამის შემდეგ გადაათეთროთ. თეთრი ფურცლები სწორდება იმიტომ, რომ შავი ფურცლების გასწორება შეუძლებელიც კი არის, იმდენად გადახაზული და სხვადასხვა პრობლემის მატარებელია. დაბეჯითებით გთხოვთ, გადათეთრებისას, არ დაუშვათ ისეთი ლაფსუსი, როგორიც ამ აბიტურიენტმა დაუშვა. სავარაუდოდ, მან სწორად ამოხსნა რადიუსი, მაგრამ არ გადმოიტანა ეს გზა თეთრ ნაწერში და ყოველგვარი მსჯელობის გარეშე დაწერა, რომ რადიუსი უდრის 3-ს.
მაგალითად, პირველ ამოცანაში, №37, აბიტურიენტს მოცემული აქვს წრფე, წრფის განტოლება, მან ეს მოცემულობაში ჩაწერა და ეს წრფე ეხება წრის სექტორს, რომლის ცენტრი მდებარეობს კოორდინატთა სისტემის სათავეში, უნდა ეპოვა წრის რადიუსი. ყოველგვარი დასაბუთების გარეშე, დაწერა, რომ რადიუსი არის 3 ერთეულის ტოლი. სინამდვილეში, ეს ამოცანა რომ ამოვხსნათ, რადიუსი მართლაც 3 ერთეულის ტოლია და მან, სავარაუდოდ, ეს სავარჯიშო ფურცელზე შეასრულა, მაგრამ არ გადმოიტანა თეთრ ფურცელზე. ამ დროს, ჩვენ უნდა ვიცოდეთ, მეგობრებო, რა გზით მიხვედით პასუხამდე. სავარჯიშო ფურცლები გამსწორებლებს არ მისდის, ეს მხოლოდ თქვენთვის არის გამოყოფილი, რომ ამოცანის ამოსახსნელად სხვადასხვა გზა მოსინჯოთ და მხოლოდ ამის შემდეგ გადაათეთროთ. თეთრი ფურცლები სწორდება იმიტომ, რომ შავი ფურცლების გასწორება შეუძლებელიც კი არის, იმდენად გადახაზული და სხვადასხვა პრობლემის მატარებელია. დაბეჯითებით გთხოვთ, გადათეთრებისას, არ დაუშვათ ისეთი ლაფსუსი, როგორიც ამ აბიტურიენტმა დაუშვა. სავარაუდოდ, მან სწორად ამოხსნა რადიუსი, მაგრამ არ გადმოიტანა ეს გზა თეთრ ნაწერში და ყოველგვარი მსჯელობის გარეშე დაწერა, რომ რადიუსი უდრის 3-ს.
იგივე ეხება ქვემოთ მოთავსებულ 34-ე დავალებას. ეს ტექსტური დავალებაა და აქაც პირდაპირ ჩანს, რომ პირველი წევრი არის x, მეორე წევრი – x + 6, მესამე წევრი – x + 36, ამის შემდეგ არავითარი განტოლება არ არის შედგენილი, არავითარი მსჯელობა არ ახლავს, უბრალოდ ჩამოწერილია პასუხები: პირველი წევრი – 1, 5 და ა.შ. ეს პასუხები კიდეც რომ იყოს სწორი, როგორც გითხარით, ინსტრუქცია მოითხოვს ლოგიკურად გამართული მსჯელობის შედეგად მიღებულ პასუხებს და შესაბამისად, შეფასება იქნება 0 ქულა. ამიტომ, ჩვენი რჩევაა, თქვენი ნააზრევი და ქმედებები გადმოეცით ნათლად და თანმიმდევრულად, მკვეთრი ნახტომების გარეშე. მკითხველისთვის ნათელი უნდა იყოს თქვენ მიერ ჩატარებული ამოხსნის გზა და გამოთვლები. ნაწერიდან უნდა ჩანდეს, როგორ მიიღეთ ამა თუ იმ სიდიდის მნიშვნელობა.
კიდევ ერთი ხარვეზი, რომელიც ასევე ხშირად გვხვდება და მინდა თქვენი ყურადღება შევაჩერო. 31-ე დავალება პარამეტრული დავალებაა, ოღონდ პირველი რიგის განტოლება. რატომღაც აბიტურიენტები მათემატიკური ობიექტის ამოცნობას იმდენად დიდ ყურადღებას არ აქცევენ, რაღაცას მიამსგავსებენ და შემდეგ იყენებენ მათთვის ცნობილი სიტუაციისთვის დამახასიათებელ სიდიდეებს. მაგალითად, თუ საკითხი ეხება სამკუთხედს, ახსენდებათ პითაგორას თეორემა და რატომღაც თვლიან, რომ ეს სამკუთხედი მართკუთხაა და ცხადია, თუ მართკუთხა არ არის და დაწერ პითაგორას თეორემას, სასურველ შედეგს ვერ მიიღებ.
 აქ, რატომღაც, ამოცანის ამოხსნის ავტორს გაახსენდა, რომ კვადრატულ განტოლებას ახასიათებს დისკრიმინანტი და თუ დისკრიმინანტი 0-ზე ნაკლებია, სკოლიდან იცის, რომ მას არ გააჩნია ამონახსნი ნამდვილ რიცხვებში (ცხადია, ნამდვილი რიცხვების მეტი სხვა არ იციან სკოლაში), ამიტომ წერს, რომ დისკრიმინანტი უნდა იყოს 0-ზე ნაკლები. ამ დროს, ეს არის წრფივი განტოლება და არავითარი დისკრიმინანტი აქ განმარტებული არ არის. ამიტომ, ჩვენი რჩევაა, ყურადღებით გაეცანით ამოცანის პირობას, სწორად ამოიცანით პირობაში მოცემული მათემატიკური ობიექტები და ამოცანის ამოხსნის პროცესში გამოიყენეთ შესაბამისი მათემატიკური დებულებები და ფორმულები.
აქ, რატომღაც, ამოცანის ამოხსნის ავტორს გაახსენდა, რომ კვადრატულ განტოლებას ახასიათებს დისკრიმინანტი და თუ დისკრიმინანტი 0-ზე ნაკლებია, სკოლიდან იცის, რომ მას არ გააჩნია ამონახსნი ნამდვილ რიცხვებში (ცხადია, ნამდვილი რიცხვების მეტი სხვა არ იციან სკოლაში), ამიტომ წერს, რომ დისკრიმინანტი უნდა იყოს 0-ზე ნაკლები. ამ დროს, ეს არის წრფივი განტოლება და არავითარი დისკრიმინანტი აქ განმარტებული არ არის. ამიტომ, ჩვენი რჩევაა, ყურადღებით გაეცანით ამოცანის პირობას, სწორად ამოიცანით პირობაში მოცემული მათემატიკური ობიექტები და ამოცანის ამოხსნის პროცესში გამოიყენეთ შესაბამისი მათემატიკური დებულებები და ფორმულები.
აი, ეს იყო სულ, ძვირფასო აბიტურიენტებო, რისი თქმაც მინდოდა. ვიმედოვნებ, რომ ჩვენი რჩევები დაგეხმარებათ, უკეთ შეასრულოთ მათემატიკის ტესტი 2021 წელს და არ დაუშვათ ის შეცდომები, რომლის შესახებაც დღეს ვისაუბრეთ. გისურვებთ წარმატებას, სტუდენტობა მოგველოცოს სექტემბრის თვეში!






