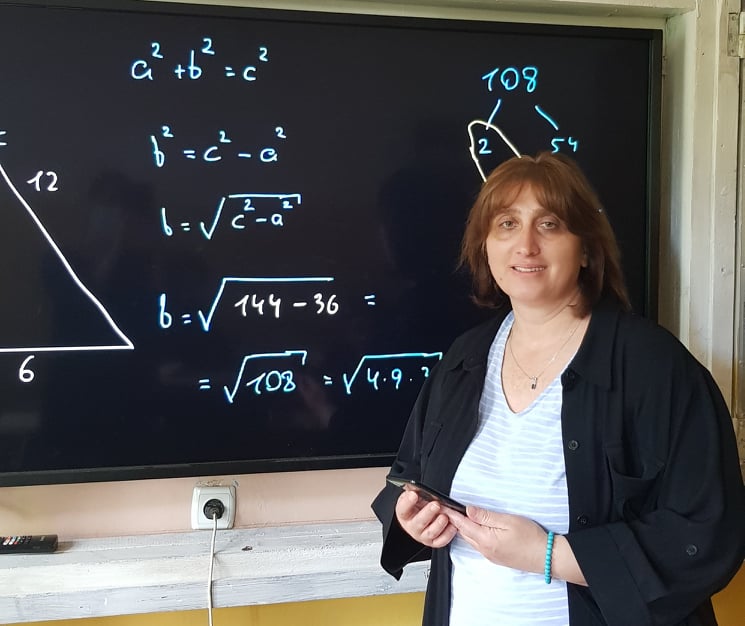ბავშვებო, ეს პატარა წერილი დაგეხმარებათ მათემატიკის უსასრულო სამყაროში კიდევ ერთი მნიშვნელოვანი საკითხის გარკვევაში.
მათემატიკა, ისევე, როგორც ძალიან ბევრი მეცნიერება, ძველ საბერძნეთში, ფილოსოფიისაგან წარმოიშვა. მათემატიკა სწავლას ნიშნავს, მათემატიკოსი კი _ სწავლულს, განსწავლულს, სწავლის მოყვარეს. ასეთი ამბიციური სახელი მეცნიერების ამ დარგს ტყუილად არ ეწოდა.
დღეს უნდა გაგცნოთ ერთ-ერთი გამორჩეული მათემატიკოსი და ფილოსოფოსი პითაგორა. პითაგორა თავისი თეორემითაა ცნობილი, მაგრამ ამჯერად მის მწირ ბიოგრაფიას გავადევნოთ თვალი.
პითაგორა არც სახელია, არც გვარი. მისი თარგმანი ასეთია: ის ვისზეც იწინასწარმეტყველა პითეამ. პითეა იყო დელფიის ორაკული, რომელმაც იწინასწარმეტყველა დიდი მათემატიკოსის დაბადება. გადმოცემების მიხედვით, პითაგორა ძველი წელთაღიცხვის მეექვსე საუკუნეში ცხოვრობდა, მასზე ინფორმაციები გვხვდება ასეულობით წლის მერე, როცა ეს ცნობილი მეცნიერი გარდაიცვალა.
პითაგორას დაუარსებია მისტიკურ-სამეცნიერო საზოგადოება „პითაგორელები“. მას უწოდებდნენ რიცხვების მამას. ყველა პითაგორელს სწამდა, რომ სამყაროში ყველაფერი მათემატიკასთანაა კავშირში და წინასწარ განჭვრეტაც შეიძლება მათემატიკით. სხვათაშორის, არაერთი მკვლევარი თვლის, რომ ქართული ანბანიც კი პითაგორელების გავლენითაა შექმნილი.
ახლა კი წმინდა მათემატიკურ ჭრილში შევხედოთ პითაგორას.
ცნობილი თეორემა, რომელიც 26 საუკუნეა, არ კარგავს თავის აქტუალობას, გულისხმობს იმას, რომ ჰიპოტენუზის კვადრატი თუ ტოლია კათეტების კვადრატების ჯამისა, სამკუთხედი აუცილებლად იქნება მართკუთხა. სიმბოლურად პითაგორას თეორემა ასე გამოისახება:ნებისმიერ სამი დადებითი რიცხვისთვის a, b, და c სადაც a2 +b2=c2., არსებობს სამკუთხედი გვერდებით a, b და c, და ყოველ ასეთ სამკუთხედს აქვს მართი კუთხე გვერდებს a და b შორის.
ცნობილია პითაგორას რიცხვებად წოდებული სამეულები:
(3, 4, 5); (5, 12, 13); (8, 15, 17); (7, 24, 25); (20, 21, 29); (12, 35, 37); (9, 40, 41); (28, 45, 53); (11, 60, 61); (16, 63, 65); (33, 56, 65); (48, 55, 73); (13, 84, 85); (36, 77, 85); (39, 80, 89); (65, 72, 97).
ახლა კი გთავაზობთ საინტერესო მიგნებებს. ამ მიგნებების დასამტკიცებლად გამოიყენეთ წრეობრივი ან კლუბური მუშაობის დროს პრეზენტაცია თქვენთვის საინტერესო და სასურველი ფორმით.
მიგნება 1. თეორემის დამტკიცებასთან ერთად, პითაგორიელებმა მიაგნეს ე.წ. „პითაგორას“ რიცხვებს (n, (n2-1)/2, (n2+1)/2, სადაც n კენტი რიცხვია) სამეულის უსასრულო მწკრივის პოვნის წესს.
მიგნება 2. მოგვიანებით აღმოჩენილი იქნა აგრეთვე სხვა დამოკიდებულებები, რომლებიც იძლევა, „პითაგორას რიცხვების“ პოვნის საშუალებას. პლატონის თანახმად, „პითაგორას“ სამეული შეიძლება მოიძებნოს შემდეგი სახითაც: n, (n/2)2-1, (n/2)2+1, სადაც n ლუწი რიცხვია.
ხათუნა სვანაძე – ფარცხანაყანევის N1 საჯარო სკოლის მათემატიკის მასწავლებელი